
As can be observed in the diagram, the areas formed when the earth is closest to the sun can be approximated as a wide but short triangle whereas the areas formed when the earth is farthest from the sun can be approximated as a narrow but long triangle. For instance, if an imaginary line were drawn from the earth to the sun, then the area swept out by the line in every 31-day month would be the same. Yet, if an imaginary line were drawn from the center of the planet to the center of the sun, that line would sweep out the same area in equal periods of time. A planet moves fastest when it is closest to the sun and slowest when it is furthest from the sun. The speed at which any planet moves through space is constantly changing. Kepler's second law - sometimes referred to as the law of equal areas - describes the speed at which any given planet will move while orbiting the sun. Kepler's first law is rather simple - all planets orbit the sun in a path that resembles an ellipse, with the sun being located at one of the foci of that ellipse. In fact, a circle is the special case of an ellipse in which the two foci are at the same location. The closer together that these points are, the more closely that the ellipse resembles the shape of a circle. The two other points (represented here by the tack locations) are known as the foci of the ellipse. An ellipse is a special curve in which the sum of the distances from every point on the curve to two other points is a constant. Then begin to trace out a path with the pencil, keeping the string wrapped tightly around the tacks. Take your pencil and pull the string until the pencil and two tacks make a triangle (see diagram at the right). Then tie the string into a loop and wrap the loop around the two tacks. Tack the sheet of paper to the cardboard using the two tacks. An ellipse can easily be constructed using a pencil, two tacks, a string, a sheet of paper and a piece of cardboard. Kepler's first law - sometimes referred to as the law of ellipses - explains that planets are orbiting the sun in a path described as an ellipse. The ratio of the squares of the periods of any two planets is equal to the ratio of the cubes of their average distances from the sun.
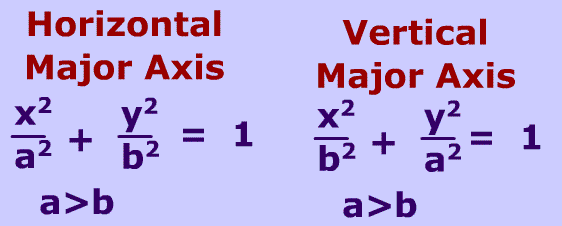
An imaginary line drawn from the center of the sun to the center of the planet will sweep out equal areas in equal intervals of time.The path of the planets about the sun is elliptical in shape, with the center of the sun being located at one focus.Kepler's three laws of planetary motion can be described as follows:


Kepler's efforts to explain the underlying reasons for such motions are no longer accepted nonetheless, the actual laws themselves are still considered an accurate description of the motion of any planet and any satellite. Kepler was able to summarize the carefully collected data of his mentor - Tycho Brahe - with three statements that described the motion of planets in a sun-centered solar system. In the early 1600s, Johannes Kepler proposed three laws of planetary motion.


 0 kommentar(er)
0 kommentar(er)
